Logistic regression

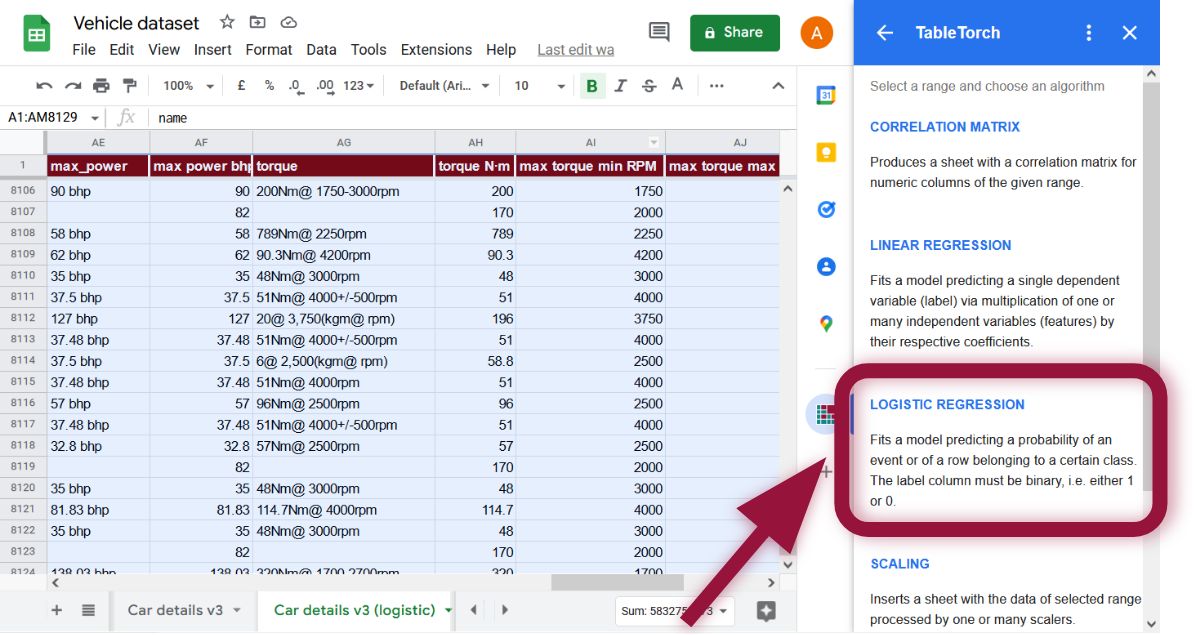
Logistic regression fits a model predicting the probability of the row belonging to a certain class.

For example, in a dataset of factory’s machinery, it is possible to predict the probability of an equipment failure within 2 weeks without urgent maintenance, helping the team focus on equipment needing promptest attention. Other examples include predicting customer churn, employee turnover, client’s interest in particular topic. Possibilities are endless.

Watch on YouTube: Binary classifier | Logistic regression | Real-world business data analysis 18:17

Logistic regression is a special kind of linear regression. It requires that the dependent variable (label) is either 1 or 0, denoting whether the record belongs to the class or not, and fits a linear model that has its label transformed with logistic function.

Logistic function is defined as follows:

During the estimation, this formula is applied with arguments of

L = 1
k = 1
x0 = 0

whereas x is the result of linear model’s estimation. Thus, predictions of logistic model belong to the set of (0; 1) and can be interpreted as probabilities of the row belonging to the class.

Logistic curve

TableTorch provides the same advanced feature set for performing logistic regressions as it does for linear regressions. For more information about various learning and sampling options, see the fine-tuning regressions page.

In the following sections, we will fit logistic model predicting whether the selling_price column of vehicle dataset exceeds 1,025,000 which is a 90th percentile of this column.

Start TableTorch

Install TableTorch to Google Sheets via Google Workspace Marketplace. More details on initial setup.
Click on the TableTorch icon on right-side panel of Google Sheets.

Identifying expensive vehicles

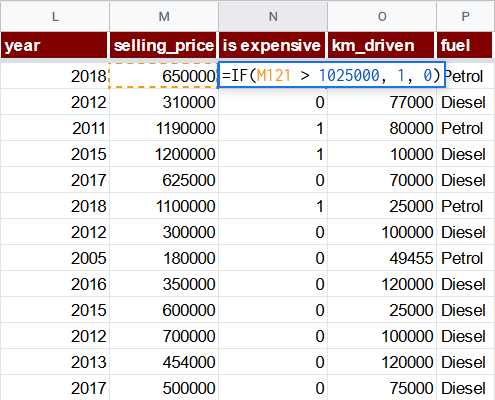
Add is expensive column after the selling_price with a formula

=IF(M2 > 1025000, 1, 0)

"is expensive" column

Select the whole range of the sheet and click Logistic regression menu item inside TableTorch.

Set is expensive column as the label. Additionally, uncheck selling_price column in the features list because our label depends on it so it should not be used in a regression.

Selecting label for logistic regression

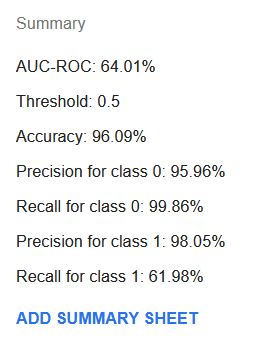
Click Fit model to perform the regression. The regression summary will appear shortly and should look like the following:

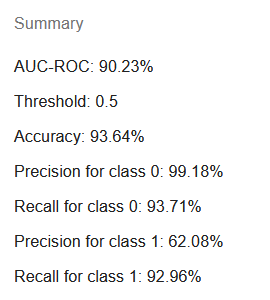
Logistic regression summary

Notice that shown characteristics are different from those that appear for linear regressions. This is correct, it does not make much sense to estimate RMSE or R² because we are more interested in the accuracy of class identification rather than exact residual between the prediction and 1 or 0 of the label.

AUC-ROC (area under curve - receiver operating characteristic) is an often used metric to estimate the probability of the model’s prediction being correct.

Threshold is always 0.5 by default and is present in the summary because the following metrics such as accuracy, precision and recall depend on it. Binary classifiers based on logistic models assign class for rows having prediction greater or equal to the threshold.

In a later section of this document, we’ll review the detailed summary sheet of logistic regression that might help us choose a different threshold based on our priorities.

Accuracy represents the share of rows for which the model succeeded in giving the right answer.

Precision for class 0 and precision for class 1 show the percentage of rows predicted to belong to certain class correctly. For example, if precision for class 1 is 62%, it means that 38% of rows predicted to belong to class 1 did not actually belong to it, indicating a significant rate of false positives.

Recall for class 0 and recall for class 1 mean the share of rows observed to be in particular class and also predicted by the model to be in this class. For example, if recall for class 1 is 93% then 7% of rows observed to belong to class 1 were given inaccurate prediction.

Click Insert prediction column button. The produced column’s value for each row will represent model’s estimation of a probability that this vehicle has the selling_price higher than 1,025,000.

Having this probability, it is now possible to insert a binary classifier column, the only important parameter that is yet to be determined is the threshold at which a row should be assigned the is expensive class:

=IF(AN2 >= 0.5, 1, 0)

Number 0.5 in the formula above is the threshold in question. 0.5 is often giving the most balanced performance for the model in terms of recall, precision, and accuracy. However, depending on our aims, a different value might be more suitable.

Let’s click Add summary sheet button and review the details of the regression.

In addition to the intercept and coefficients that are present on the summary for any linear regression, the summary sheet for logistic regression contains the table of precision, recall, and accuracy characteristics at various threshold levels.

For example, if we’d like the model to be more precise and avoid erroneously assigning class 1 to rows, we might consider using the threshold of 0.87 instead of 0.5 because the precision at that point reaches 90% in place of mere 62% for the threshold of 0.5. However, we also see that at threshold 0.87 the recall drops to just under 80% which is much less than almost 93% achievable for the threshold of 0.5.

In the same fashion, choosing a lower threshold, e.g. 0.13, can significantly improve recall of the classifier, reaching almost 99% at the cost of reducing the precision to around 40%.

There is, however, a possible way to achieve the desired level of precision or recall without sacrificing the other characteristic: producing a better model.

Tuning the logistic regression

Every possible option discussed on the page about fine-tuning linear regressions is applicable to logistic regressions as well because under the hood, the process is the same.

Let’s try the following tuning steps:

Apply the feature engineering and column exclusion techniques described on fine-tuning regressions page.
Turn on 3-Fold Cross-Validation.

Add more manufacturer identifying columns in the same fashion as we did during the preparation of the vehicle dataset.

Volvo
```
=IF(ISNUMBER(FIND("Volvo", A2)), 1, 0)
```
BMW
```
=IF(ISNUMBER(FIND("BMW", A2)), 1, 0)
```
Audi
```
=IF(ISNUMBER(FIND("Audi", A2)), 1, 0)
```

Mercedes-Benz

=IF(ISNUMBER(FIND("Mercedes-Benz", A2)), 1, 0)

Lexus
```
=IF(ISNUMBER(FIND("Lexus", A2)), 1, 0)
```

Jaguar

=IF(ISNUMBER(FIND("Jaguar", A2)), 1, 0)

Jeep
```
=IF(ISNUMBER(FIND("Jeep", A2)), 1, 0)
```

Land Rover

=IF(ISNUMBER(FIND("Land Rover", A2)), 1, 0)

Volkswagen

=IF(ISNUMBER(FIND("Volkswagen", A2)), 1, 0)

Add more derived features:
- perceived wear
```
=Z2 / (Y2 / MAX($Y$2:$Y$8129))
```
where Z is the km_driven column and Y is the average price of year column.
- depreciated torque N·m
```
=AU2 * Y2 / MAX($Y$2:$Y$8129)
```
where AU is the torque N·m column and Y is the average price of year column.
Select the whole range and open the Logistic regression tool in TableTorch.
Use stratified uniform random sampling with year stratum as stratum column.
Unselect *year, selling_price, is expensive, km_driven, petrol, max power bhp, engine cc, torque N·m, max torque min RPM** columns from the features list.
Click Fit model.

The produced model will have a summary like this:

Although AUC-ROC has become quite lower at 64%, accuracy, recall for class 0 and precision for class 1 have greatly improved. Recall for class 1 has fallen significantly to just 62% but if we look at the learning summary sheet, it is possible to find a threshold, e.g. of 11% where recall is at 83% while the precision is at 89% and the accuracy is at 97%.

The new model is probably a better one than that achieved with default settings but it still does not look as a significant improvement. Perhaps, the dataset will need additional original features indicative of an expensive vehicle so that it would be possible to fit a more precise model.

Stratification

TableTorch uses stratified uniform random sampling for logistic regressions by default in order to produce an unbiased model. However, it might not always be desirable since the performance of such a model would likely be tailored to recall characteristic for the underrepresented class (1 in case of is expensive column is assigned to just 10% of the records).

Hence, if stratified proportional random sampling is used, the regression will likely be more precise on average. For our example, the usage of proportional sampling will result in a model with AUC-ROC of just 27%, however, it will also have the precision for class 1 at 98.4% at threshold of 0.05 with a recall for class 1 at 62%. Such a model might not be great at identifying every expensive vehicle but when it does indicate that the vehicle is expensive, chances are high that this is actually the case.

Let us know!

Thank you for using or considering to use TableTorch!

Does this page accurately and appropriately describe the function in question? Does it actually work as explained here or is there any problem? Do you have any suggestion on how we could improve?